Les fleurs et les nombres .
Avez vous déjà regarder avec attention la position des pétales de fleurs sur leur cœur ?
Comptez les pétales des fleurs que vous apercevez. Dans la plupart des cas, le nombre auquel vous arriverez sera l’un de ceux-ci, ou alors un nombre qui s’en approche : 1, 2, 3, 5, 8, 13, 21, 34, 55, 89… Un iris aura 3 pétales, un bouton d'or 5 et la marguerite 21, 34, 55 ou 89 .
Ces nombres font partie d’une série bien connue des mathématiciens, la «suite de Fibonacci», du nom de son découvreur, l’Italien Léonard de Pise, dit Fibonacci (environ 1170-1250) . Cette suite relativement simple a plusieurs propriétés remarquables. L’une d’entre elles est sa relation avec le célèbre nombre d’or.
Dans cette suite, qui commence par [1, 1], le nombre suivant est obtenu en additionnant les deux derniers de la liste. On commence donc par la somme de 1 et 1, puis on ajoute le résultat au bout de la série, qui devient alors [1, 1, 2]. On additionne ensuite 1 et 2 = 3, ce qui allonge la liste à [1, 1, 2, 3], puis on enchaîne avec 2 et 3 = 5, puis 3 et 5 = 8, et ainsi de suite, ce qui donne : 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…
Cette série de nombre est en fait omniprésente dans le monde végétal. Non seulement le nombre de pétales d’une fleur est-il généralement un nombre de Fibonacci, mais encore trouve-t-on cette suite dans bien d’autres parties de nos amies vertes.
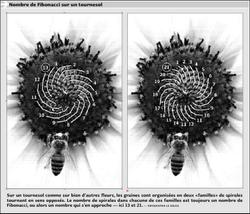
Regardez le plus spectaculaire et surtout une des plus grosses: le tournesol. Regardez la disposition des étamines qui vont donner chacune une graine.comme sur l'illustration ci-dessus, on voit aisément que les graines sont disposées de façon à former deux groupes de spirales tournant en sens opposés. Et combien de bras chacun de ces groupes compte? Deux nombres de Fibonacci consécutifs — 13 et 21 .
Les pommes de pin et les ananas, si on les regarde du dessous, montrent le même genre d’arrangement, bien que le nombre de bras de spirales soit alors plus petit.
Mais on peut trouver encore mieux.** Chez les plantes, lorsqu’une nouvelle feuille pousse le long de la tige, elle ne pousse pas au hasard, elle forme généralement un angle d’environ 137,5 degrés avec la feuille qui avait poussé juste avant elle, c'est la la phyllotaxie ou foliation.
Sur l'image de gauche on ne voit pas vraiment la disposition des feuilles, alors qu' à droite , vue de dessus c'est très spectaculaire.
Quel avantage en tirent-elles? Les hypothèses récentes tournent souvent autour du même thème général : l’utilisation optimale de l’espace.
Ainsi, des travaux ont montré qu’un angle de 137,5° permet de disposer les feuilles autour de la tige de telle manière qu’elles ne se fassent pas trop d’ombre entre elles, ce qui maximise la surface du feuillage exposée à la lumière. Si cet angle était autre, les feuilles du haut nuiraient davantage à celles du bas.
Enfin, pour ce qui est des fleurs,il semble que disposer ses graines en deux familles de spirales dont le nombre de bras est deux nombres de Fibonacci consécutifs permette d’en faire entrer un maximum dans un espace donné. Tout autre agencement comporterait apparemment des «trous».
Je vous ai déjà dit que la nature est formidable et qu'elle n'a pas fini de nous surprendre, une preuve de plus.
** Faisons d’abord des fractions avec la suite de Fibonacci, pour obtenir la série : 1/3, 2/5, 3/8, 5/13, 8/21, 13/34, etc. Si on les écrivait en décimales, on verrait que la valeur de ces fractions fluctue passablement au début, mais qu’elle finit rapidement par tendre vers environ 0,382. Maintenant, imaginons qu’avec un compas, on trace un arc de cercle équivalent à 0,382 tour. L’angle correspondant sera alors de 0,382 x 360° = 137,5°.
Sources: différents articles et sites internet résumés et assemblés. J'ai essayé d'être le plus simple possible, je ne suis pas certain d' y être parvenu, pour avoir d'autres informations >>> " fibonacci+fleurs" sur Google ou autre moteur de recherche.